Free Online Drawing Book

Lesson X. -- The Cylinder.
Connect two circular tablets by a 2 1/2 " stick, to rep resent the cylinder. Hold the object so that one end only is visible, and see that it appears a circle. (See Rule 16.)
Place the object on the desk, so that its axis is horizontal but appears a vertical line, and trace its appearance. The tracing illustrates the following rule :
Rule 19. When an end and the curved surface of a cylinder are seen at the same time, the end must appear an ellipse.
Place the object horizontally, and so that one end appears a vertical line, and trace to illustrate
the following rule :
Rule 20. When one end of a cylinder appears a straight line, the other appears an ellipse.
Place the object upright on the desk, and trace its ends and axis. Draw the long diameters of the ellipses, and discover that they are at right angles to the axis of the cylinder. This illustrates the following rules :
Rule 21. The bases of a vertical cylinder appear horizontal ellipses. The nearer base always appears the narrower ellipse.
Place the object with its axis horizontal and at an angle, so that the surfaces of both tablets are visible. Trace the tablets and the rod, and then draw the long diameters of the ellipses, and discover that they are at right angles to the axis of the cylindrical form. The axes of the ellipses are inclined, and the drawing illustrates the following rules :
Rule 22. The bases of a cylinder appear ellipses whose long diameters are at right angles to the axis of the cylinder, the nearer base appearing the narrower ellipse.
NOTE.--The farther end may appear narrower than the nearer, but must always appear proportionally a wider ellipse than the nearer end.
Rule 23. Vertical foreshortened circles below or above the level of the eye appear ellipses whose axes are not vertical lines.
Rule 24. The long axis of an ellipse representing a vertical circle below or above the level of the eye is at right angles to the axis of a cylinder of which the circle is an end.
Rule 25. The elements of the cylinder appear to converge in the direction of the invisible end. This convergence is not represented when the cylinder is vertical.
NOTE 1..--Less than half the curved surface of the cylinder is visible at any one time.
NOTE 2. -- The elements of the cylinder appear tangent to the bases and must always be represented by straight lines tangent to the ellipses which represent the bases. When the elements converge, the tangent points are not in the long axes of the ellipses. See illustration opposite Rule 19, in which if a straight line tangent to the ellipses be drawn, the tangent points will be found above the long axes of the ellipses.
Lesson XI. -- The Cone.
Hold the cone so that its axis is directed towards the eye, and the cone appears a circle. Hold the cone so that its base appears a straight line, and it appears a triangle.
Place a circular tablet having a rod attached, to represent the axis of the cone, so that the axis is first vertical, and second inclined. Trace both positions of the object, and discover that the appearance of the circle is the same as in the case of the cylinder. The tracings illustrate the rule.
Rule 26. When the base of the cone appears an ellipse, the long axis of the ellipse is perpendicular to the axis of the cone.
NOTE 1.-- More than half the curved surface of the cone will be seen when the vertex is nearer the eye than the. base, and less than half will be seen when the base is nearer the eye than the vertex. The visible curved surface of the cone may range from all to none. See illustrations on p. 77.
NOTE 2.--The contour elements of the cone are represented by straight lines tangent to the ellipse which represents the base, and the points of tangency are not in the long axis of this ellipse. See illustrations on p. 77.
Lesson XII. -- The Regular Hexagon.
In this figure the opposite sides are parallel and equal. The long diagonal A .D is parallel to the D sides B C and E F, and it is divided into four equal parts by the short diagonals B F and C E, and by the long diagonal B E or C F.
The perspective drawing of this figure will be corrected by giving the proper vanishing to the different sets of parallel lines, and by making the divisions on the diagonal A D perspectively
equal.
Draw the long and short diagonals upon a large hexagonal tablet. Place this tablet in a horizontal or vertical position, and then trace 4 upon the slate its appearance and the lines upon it. The tracing illustrates the following rule :
Rule 27. In a correct drawing of the regular hexagon, any long diagonal, when intersected by a long diagonal and two short diagonals, will be divided into four equal parts.
Lesson XIII. -- The Centre of the Ellipse does not Represent the Centre of the Circle. (For teachers only.)
Cut from paper a square of three inches, after having inscribed a circle in the square. Draw the diameters of the square and then place the square horizontally at the middle of the back of the desk, with its edges parallel to those of the desk. Trace the square, its diameters, and the inscribed circle, upon the slate. The circle appears an ellipse, and as the long axis of an ellipse bisects the short, it is evident that it must come below the centre of the square, and we discover that the centre of the ellipse does not represent the centre of the circle, and that the diameter of the circle appears shorter than a chord of the circle.
Lesson XIV. -- Concentric Circles.
Cut a 4" square from practice paper, and draw the diagonals. With the centre of the square as centre, draw two concentric circles, 4" and 2" in diameter.
Place the card horizontally upon the desk, as NI II 1st" 6101a illustrated, and trace its appearance upon the Apoimim slate, together with all the lines drawn upon it.
Draw the vertical line which is the short axis of both ellipses. Bisect the short axis of the outer ellipse, and draw the long axis A of this ellipse. Bisect the short axis of the inner
ellipse, and draw its long axis B. It will be seen that the long axes are parallel, but do not coincide, and that both are in front of the point which represents the centre of the circles.
Each diameter of the larger circle is divided into four equal parts. The four equal spaces on the diameter which appears the short axis appear unequal according to Rule 14. The diameter which is parallel to the long axes of the ellipses has four equal spaces upon it, and they appear equal. This diameter is behind the long axes, but generally a very short distance, and in practice, if the distance I, 2 between the ellipses measured on the long axis is one- fourth of the entire long axis, then the distance between the ellipses measured on the short axis must be a perspective fourth of the entire short axis. This illustrates the rule:
Rule 28. Foreshortened concentric circles appear ellipses whose short axes coincide. The distance between the ellipses on the short axis is perspectively the same proportion of the entire short axis, as the distance between the ellipses measured on the long axis, is geometrically of the entire long axis.
Lesson XV. -- Vase Forms.
Place a sphere on the desk below the eye, and having marked the highest point upon it A, see that this point does not appear in the circle which defines the sphere, but comes below or inside this circle, a distance which varies with the distance of the sphere from and below the eye.
Place the modeled sphere, from which a small section has been cut, so that the section is horizontal and at the top, and trace the appearance of the object upon the slate. Indicate the elements of a cylinder or cone tangent to the ellipse which represents the section.
The circular section appears an ellipse, and appears inside the circle which defines the sphere. This illustrates the following rule :
Rule 29. In vase forms, when a cylindrical or conical body intersects a larger curved body or portion of convex form, and the line of intersection is visible in any position of the object, the contour lines of the smaller part extend inside the contour of the larger part : thus the extremities of the long axis of the ellipse which represents the intersection are not in the contour of the larger part.
Lesson XVI. --Frames.
In the frames are found regular concentric polygons with parallel sides, the angles of the innei polygons being in straight lines connecting the angles of the outer polygon with its centre. In polygons having an even number of sides, the lines containing the angles of the polygons form diagon4ls of the figures, as in the square.
In polygons having an odd number of sides, the lines containing the angles of the polygon are perpendicular to the sides opposite the angles, as in the triangle. The figures illustrate the above facts and the rule.

Draw upon large triangular and square tablets the lines shown in Figs. A and B. Place the tablets horizontally on the desk, or support them vertically, and trace upon the slate the appearance of their edges and all the lines drawn upon them. The tracings illustrate Rule 3o.
Rule 3o. In representing the regular frames, the angles of the inner figure must be in straight lines passing from the angles of the outer figure to the centre. These lines are altitudes or diagonals of the polygons.
NOTE. -- The most important principles of the subject are stated briefly and simply in this chapter for the benefit of teachers of elementary work. Teachers of art schools and advanced classes will find the subject treated at greater length, and in a way suited to the requirements of advanced students, in the book, 4, Free-hand Drawing, Light and Shade, and Freehand Perspective," by Anson K. Cross.
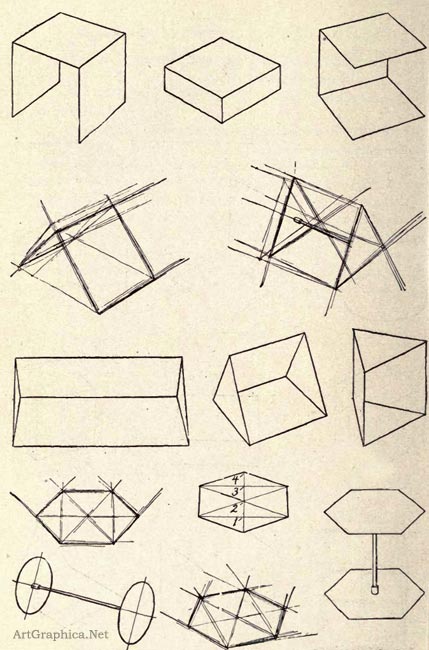
DRAWINGS ILLUSTRATING THE RULES.
The principles governing the appearance of geometric forms have been illustrated by the use of tablets. The following drawings represent both tablets and solid objects in different positions, which illustrate the rules.
The first drawings represent tablets and objects when placed upon the pupils' desks. When objects are thus placed perspective effects are often unpleasant ; therefore after the first experiments the objects should be raised from the desk. They should not be placed so as to be foreshortened less than the first objects represented below.
The drawings are reproductions of pen sketches. Some are slightly accented, but they are not given for examples of handling, for which the sketches of the pupils' drawing books must be used.
The figures in which light lines are found illustrate the appearance which drawings should have before any lines have been erased.
CHAPTER VII.
SCIENTIFIC PERSPECTIVE AND MODEL DRAWING.
(This chapter is for teachers of drawing and advanced art students.)
A PERSPECTIVE is generally understood to be a scientific perspective made upon a vertical picture plane placed between the eye of the spectator and the subject to be represented. Drawings of this nature are generally made upon paper by applying the principles of perspective. To make such a drawing it is necessary to know the forms, dimensions, and positions of the objects, to know the position of the picture plane on which they are to be represented, and also the position of the eye of the spectator, which is supposed to be fixed at one point called the station-point. Scientific perspective is as exact as geometry,-- in fact it is a branch of geometry, and its principles may be applied upon paper to a drawing of any subject, so exact that if the paper could be rendered transparent, and suspended vertically in the position of the picture plane, every line upon it would be found to appear to coincide with the line of the object which it represents when the eye is at the station-point. The drawing is, in fact, just what would be given by tracing upon a vertical' sheet of glass placed in front of the group, and in the given position of the assumed picture plane, lines to cover each line or edge of the subject as seen through the glass and from the fixed point called the station-point.
Perspective drawings may be made upon cylindrical surfaces, but the drawing generally made is supposed to be upon a vertical picture plane. The student may readily produce a drawing to illustrate the nature of a plane perspective by fixing the eye at one point in front of a window, and then tracing upon the window lines to cover the lines of whatever may be seen through the window.
Artists and illustrators have made perspective drawings for many hundred years, and these drawings have quite generally been satisfactory when geometric forms have- been represented ; but in the highest art, which represents the human figure, artists have not made scientific perspective drawings, but have drawn instead by eye the actual appearance of each figure in the subject, and thus their drawings do not require to be seen from one fixed point in order that they may represent the appearance of all the figures.
In order to understand the difference between a scientific perspective and the drawing which an artist makes of a figure or other subject not architectural, we must determine first what the eye sees, and second any points of difference that may exist between what the eye sees and a plane perspective drawing.
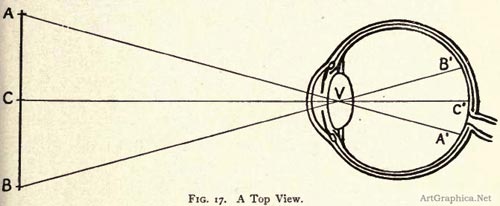
The eye contains a lens whose action is the same as that of the lens found in a camera. The rays of light from any object to the eye pass through its lens and are focused by it upon the sensitive nerves at the back of the eye. The surface of the eye which receives the light transmitted by the lens is spherical, and the rays of light pass through the lens and strike upon the sensitive retina in a direction practically perpendicular to the surface of the retina (Fig. 17).
Most of the inner surface of the eye is sensitive to the rays of light, and so the eye sees a very wide field of view. If the eye is fixed upon any object directly in front of the spectator, objects above, below, to the left, and to the right will be seen at one time, but all very indistinctly ; and though the spectator may be conscious of seeing objects at almost the extreme right and left of his position, they will be seen so indistinctly that they will not be recognized. A very small space is seen distinctly at any one time. Thus, in reading this book, it will be impossible to read a word at the left of any line and distinguish a letter at the right of the line, and only a few letters can be read without motion of the eye. The field of distinct vision is thus confined to a very small visual angle. By this is meant that the rays which come from the extreme points of what is clearly seen form very small angles with each other, and the eye cannot bring to a focus upon the retina all the rays from any object which causes large visual angles.
The rays coming to the eye from any object form a conical body whose vertex is in the lens of the eye ; passing through the lens the rays form a conical body whose vertex is also in the lens. The central visual ray, or the axis of both the cones, is perpendicular to the surface of the retina which receives it ; and the whole cone of rays which gives the image of the object is intersected by the curved surface of the retina practically at right angles to all the rays. The proportions which any object appears to have are thus dependent upon the angles between the visual rays, and the arc which measures the angle between any two rays, as those from A and B, Fig. 17, will nearly coincide with the surface of the retina.
All objects are seen by means of the images which they produce upon the retina; but any one is clearly seen only when the eye is directed to it, and thus we must accept this distinct image formed in the eye as the true picture, -- that is, as the true appearance of the object.
The retina has the general shape of a sphere, but the part that receives the rays which form a sharp image is so small that its curvature is very slight, and the image upon it is practically the same as that which would be given upon a plane surface at right angles to the axis of the cone of visual rays ; and we see that for all practical purposes we may speak of a true picture, meaning one which is similar in its form to the image of the eye, as produced by intersecting the cone of visual rays by a plane perpendicular to the central ray.
By appearance we mean, then, the image which any object produces upon the retina, and a picture which represents this appearance is a true picture. By represents is meant a picture which is similar, geometrically, to the image, so that the picture will cause in the eye the same image that the object would produce if the object were seen instead of its true picture.
The limit to the visual angle within which clear vision is possible is very small, and to see almost any object clearly the eye moves so as to be directed to its different parts ; but any object which does not create visual angles greater than 3o° will be so pictured upon the retina that when its central part is clearly seen the image is but slightly different from that which is given by intersecting the cone of visual rays by a plane perpendicular to the central visual ray instead of by the curved surface of the eye.
We must generally draw upon paper or some other flat surface, and the problem for the artist is to produce upon a plane a drawing which shall cause in the eye the nearest possible approach to the image on the curved surface of the eye which is produced by the object itself.
Seeing is a matter of education principally, and it is immaterial what the image in the eye actually is in regard to the relations of its details, for the mind reads the images by referring to the facts remembered concerning previous and similar images. Authorities on perspective state that straight lines appear curved, -- that is, cause curved images in the eye ; but it is of no consequence to the artist whether the images are curved or not, for admitting that the images are curved, the eyes of all read the images as those of straight lines, the mind supplying the knowledge of straightness whenever the images are produced by lines which are known to be straight. When curved images in the eye are produced by lines which are not known to be straight, the mind receives the impression of curved lines in nature, and the artist would represent the lines by curved lines ; but if he represents by curved lines lines which the mind knows to be straight, his drawing will not create the same impression as the image in the eye caused by the actual lines ; for if the images of the eye are curved the mind does not know it and reads them always as straight. The eye is simply a mechanical instrument, and we see much more through the mind than by study of the proportions of the image in the eye as if it were a drawing or a map.
The problem for the artist is, then, to produce a drawing which shall, as nearly as possible, cause in the eye the same visual angles as the object, and which shall at the same time cause the mind to bring forward, as far as possible, the same ideas concerning the object that the object represented would create ; and this drawing must be made upon a plane surface.
Having decided that the image in the eye -- the appearance of the object--must be considered a true picture of the object, and that it is practically what is given by intersecting the visual rays by a plane perpendicular to them, -- that is, to the central ray to any object, we will study the drawings which are given upon the vertical picture plane, generally used in scientific perspective, to discover any points of difference between them and what the eye sees. The illustrations used will generally be from photographs, for the camera gives an exact perspective drawing in which the negative corresponds to the picture plane and the centre of the lens to the station-point.
All the illustrations of this chapter, except those in outline, are reproduced directly from photographs. Photographs which represent objects causing visual angles greater than 3o° are always distortions, and when the visual angles represented are as large as 6o° or 9o° the distortions are generally very noticeable and very unpleasant. Photographs taken with lenses which include angles of from 6o° to 90° are as common as those which represent smaller angles and thus give more nearly what the eye sees. The photographs from which the illustrations of this chapter are taken do not distort more than the photographs and illustrations which are always to be found in the common representations of interiors and exteriors, and often such representations present greater distortions than these illustrations.
The illustrations of this chapter are smaller than the original photographs, and thus they should be seen from a shorter distance than the photographs. But still they are not more distorted than many drawings which are made for illustrations by those who make scientific perspective drawings instead of drawing by eye, and by those who draw from nature with the false ideas of the appearance of form which are given by study of scientific perspective without that of the free-hand perspective ; and often illustrative drawings
are more distorted than pose of this chapter.
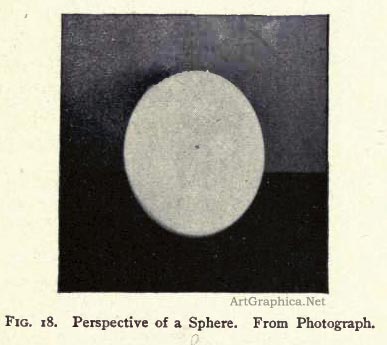
Fig. 18 is from a photograph of a sphere which was placed directly below the camera and upon a horizontal surface. The camera was horizontal, so the negative -- that is, the picture plane – was vertical. The picture of the sphere is seen to be a vertical ellipse, and it does not create a satisfactory impression of the round object.
PREVIOUS PAGE
|












