Water Reflections |
||||||||||||||||
|
Page 15 / 25
 CHAPTER XIVTHE PERSPECTIVE OF REFLECTIONSREFLECTIONS in water. — Perspective of colour has not been considered in this book. Moreover, it is impossible here to make an exhaustive study of those amazing effects in reflection caused by movement in water. All this has been searchingly inquired into and lucidly explained in that beautiful book, " Light and Water," by Sir Montague Pollock. That work should be read to supplement the bald facts that every painter must know. Reflections in smooth water. — Theory. —Rule : " The angle of reflection is equal to the angle of incidence " (Fig. 279). Let us take one point of an object to be reflected, and call it the "object." 
But the reflection of the object does not as shown in Fig. 279, but at X (Fig. 280). really appear to be at Z, as shown in Fig. 279, but at X (Fig. 280). 
It will be seen that X is on a continuation of the reflecting ray, and that it is the same depth below the surface of the water as the object is high above the water. Practice. — Rule A. Find the surface of the water immediately under each point to be reflected. Rule B. The reflection of each point will be on a vertical line dropped from that point. Rule C. The reflection of each point appears to be as far below the surface of the water (directly uncler it) as each point to be reflected is above the surface of the water (Figs. 279 and 280). Rule D. The image in water of an object is found by reflecting each of its essential points one at a time, and then joining them in the image as they are joined on the object.
Example of Rules A, B, C, D (Fig. 281). — An upright stick standing out of a sheet of water.
FACE The point 3 is now the reflection of the top of the stick. Join 3 to 1 to complete image. Another example (Fig. 282). An up right post standing out of a sheet of water. Practice. — Mark where the water surface touches the near side of post (at 1). Drop verticals from every point to be reflected. Measure the height from the water surface to top of post, repeat same measurement below the surface (1-3) on the vertical lines, and so obtain the two edges of the near side of post ; join them to make the reflection of the top line. Now mark the surface of the water where it touches the far side of post (at 4). Measure height of post (4 to 5) above surface at this point and transfer it to below surface (4 to 6). Join the corners (6 to 3) of the post. If we repeat Fig. 282 by Fig. 283 and continue the receding lines of the reflection we find they tend to the same V.P. as the lines they are the image of ; and this is always the case when the lines are in Nature level lines, so we can add Rule E. Rule E. Reflected lines. — The reflection of a line that is in Nature level, tends to the same V.P. as the line it reflects. Much labour in measuring can be saved by remembering this. For instance, in Fig. 283 a receding line from V.P. to corner 3 would decide the length of line 4-6. Rules A to D apply equally well to lines that are not level. Fig. 284 represents a post leaning to one side of us.
Transfer that length below surface 2-4. Join reflected top of post (4) to where post rises from water (5). Fig. 285 represents a post leaning towards us. In this case, in order to find where the surface of the water would be under the top of post, we must guess where a pebble dropped from its top would splash (say line 1) then carry on as before. In Fig. 286 the post leans to the side and from us. Guess the splash as before (same rules). A stick leaning to the right and projecting from a mound affords another example (Fig. 287). Practice. — Find where surface of water would be under bottom of stick (1). Drop verticals from any point to be reflected. Measure their height above surface (2-3, for example), and repeat them (on verticals) below surface (2-4). Try the same rules for a curly stick (Fig. 288). When you first sketch from Nature you may:think I mislead you in these rules, because the view you get of an object is often so entirely different from the view the water gets (excuse the expression) of the object, and this will account for apparent discrepancies that your wits alone must account for. 
The reflection of objects distant from the water. — We have said that the image of each point to be reflected, is as far below the surface of the water directly under it as the point itself is above the water surface. When objects do not rise out of the water but are distant from it, we must imagine the water to be continued till it is at their foundations, or the foundations of the ground they rest on ; this done, we proceed as before. 
Fig. 290 shows a post set back on the embankment. The height of the embankment is repeated in the reflection, but only a part of the post is reflected.
There will be sufficient accuracy in a composition done without reference to Nature by this habit of imagining water to replace the land surface. With Nature before one it will prevent the occurrence of absurd mistakes. The punts in Fig. 291 and Illus. LXI are useful illustrations of the rules taught by the less interesting Figs. 286 and 287.
Our delight in watching still water is often due to the tricks its surface. seems to play on us. In it appears, perhaps, the underside of a footbridge we look down upon, or the dark lower surface of overhanging leaves instead of their sunlit tops. The water sketches, as it were, an important bank outlined dark and sharp against a clear sky as the reflected picture of an insignificant river-edge and miles of flat country. Objects that are in Nature hidden from view by others intervening, appear in the water side by side with distant and near ones, and yet nothing is haphazard, but all conform to the ever-lasting laws of Nature. Reflections of an archway or bridge. — The same rules apply to the reflection of arches. Practice. — Draw the bridge (Fig. 293) and a line along the surface of the water where it touches the near side of the bridge 1-2, and a corresponding one on the far side 3-4. These lines will be under the face of the arch on the near side and the far side of the bridge respectively, and consequently will mark the surface of the water beneath each. We can now drop verticals (line A–B, Fig. 294) from any point to the surface to find how far below the 'surface (line B–C) the reflected point will come. If there are projecting buttresses remember to draw additional similar lines where they touch the water surface.
Reflections in a raised canal or pond on a hill-top. Standing by a hill-top pond with the sloping land stretching to the distance one is for a moment disconcerted to find only the sky or bordering trees reflected. The reason for this is clear enough when we recall our rules. If in Illus. LX1I, for instance, we continue the surface of the water we see that it could never come dircctly under the distant trees, in fact it would be above the level of their tops, and so they cannot be reflected. This does not apply to the tops of the trees higher up the slope, and we see their reflection. 
Reflections in rippled water. — Our notes on the angle of incidence and reflection still hold good. The law that a reflected point is somewhere on a vertical line under the point itself also may stand. The law as to the relative height of an object and its reflection must be modified. The chief differences between still and slightly rippled water are : (1) the image instead of repeating the height of an object may be elongated ; (2) the image is incomplete or interlined with the reflection of another object, or by different parts of the same object ; (3) in the distance the object is often more closely resembled than in the nearer reflection ; (4) vertical objects are seen in the reflection, when narrow horizontal ones are not repeated. (1) Lengthening of the image. Let Fig. 296 represent the length of the reflection of the tree as seen by the painter. Let Fig. 297 also show this, but with a ripple in the painter's foreground. He will see a portion of the ripple turned partly away from him, and in this new plane the reflection of the tree. This accounts for the reflection appearing longer, as in Fig 299. 
(2) We account for the image being broken or incomplete by Fig. 298. The ripples in it have several planes, and each of these planes reflects at a different angle. The reflection from two planes of the ripples only are shown to save confusion. (3) This also supplies a reason for the closer repetition of the imags far away, though another common cause is that the edges of the river or lake are less ruffled than the outlying surface. 
(4) Horizontal and vertical lines. Horizontal lines being missed in the reflection, though vertical ones are shown. Perhaps this is the most characteristic quality of rippled water. In Fig. 301 let us suppose an upright post or wall and the dots to be horizontal bars. The reflections of these bars could only appear a certain distance (A). If a ripple occurs at these points it destroys the reflection of a bar, but one of the many planes on the ripple is sure to catch some part of the wall. The part it catches might be higher up or lower down than that part reflected in still water. It is an everyday experience to see the upright posts of a railing reflected but the image of the rails missing. The lengthening of an image vertically is often due to the same spot being reflected in various planes of successive ripples, and so at night we get those beautiful lines of height stretching towards us from the harbour lights. Reflection of the moon. — These pathways of light are roughly the same width that the object throwing them appears to be. One notices this fact in the lengthening reflection from the moon on slightly rippled water. On rougher water the reflection will be caught by the sides of waves outside the regular path, and so extended horizontally to a wider and less sharply defined streak. It is a mistake to think of this streak of light literally as a silver path on the surface of the water ; if it were so, its sides would converge towards the horizon. The width of the streak varies as the moon is high or low, and it may be deflected to one side by waves running that follow the line of the horizon. 
Note. — Though we said that reflections are always vertically under the objects, I have noticed one is apt unconsciously to represent the reflection of vertical lines as very slightly inclined towards the spot we stand on, and I have seen them so painted, and I think rightly so, by artists of repute. In the harbour when the water heaves with a gentle swell, we see effects that seem to contradict every rule of still-water reflections. Wonderful loops, half-circles, and zig-zags as the reflections of an upright mast or even bits of images not upside down but as the object, the latter phenomenon being accounted for by the curves in the water acting as a convex mirror would. Reflections in a mirror. — The same rules by which we copy an image in still water have to be used (A) when the reflection is given by a mirror with its surface in the same plane as water (i.e. level). Therefore we need not repeat the instructions when the mirror lies in a level position below us. (B) If the mirror stands in a vertical position (Fig. 302) on one side of us, we carry horizontal lines across from each point to be reflected, till they touch the mirror's surface and continue them the same distance beyond, to fix the reflection of the point. When each point is reflected and joined, it will be seen that the receding lines in Nature and their reflection have the same vanishing points[1]. (C) The reflection in a mirror lying level above the height of our eye is subject to the same rules as one lying below the height of our eye. The chief difficulty is getting used to carrying lines up to the mirror's surface instead of downwards. In the case of A, B, C, if the mirror is a small one or nearer to you than the object you must continue its surface until it is (for A) under, (for B) opposite, or (for C) over the object, as the case may be, just as you continue the surface of water until it is under the object. Refraction. — We see the most perfect reflections when our head is near the level of the water ; the reason being that our eye receives the greater number of rays that are reflected from the water surface, and it does not perceive the colour of the water or stones at the bottom, which become visible by refracted rays. 1. A man of science explained this to me most admirably. " Think of a room furnished and arranged exactly the same at one end as at the other ; let it be divided through the centre by a sheet of glass: The half of the room you sec through the glass may be considered as the actual reflection of the other half, and can he drawn by perspective rules just as if it were the room itself." Some rays of light as they strike the surface of water are reflected, the remainder refracted ; that is, they enter the water and continue their course still by straight lines, but at an angle in a more vertical direction towards the bottom. It follows that if we retrace the course of a refracted[1] ray from a stone on the river-bed, that it reaches the water's surface by a straight line, and leaves it by another that is less vertical, and so reaches our eye. When we look at the water we do not reason out this angle in the rays' journey, but we think we see the stone on a continuation of the straight line from our eye ; and are deceived into thinking the stone to be nearer the surface than it actually is. The reason for reflections appearing more perfect as we approach the level of the water is that more of an oblique ray is reflected, and less refracted, than of one that strikes the water in a more vertical position. The lines of foreground rocks, water plants, and objects partly submerged constantly show the refraction. They are often beautiful and should be studied, and a beginning might be made by looking at Millais' " Ophelia," and by observing such commonplace effects as a slanting stick with its submerged end appearing to be tilted upwards. 1. The laws of reflection and refraction as given in text-books on science, must be accepted with reserve, for the reason that the alteration in the appearance of lines from perspective is not considered. Often more can be learnt by a stick, a pail of water, and a looking-glass, than by books which are not written for artists.
Next Page
How to Draw Shadows Prev Page Sky in Perspective
|
||||||||||||||||
Practice. - First mark where the surface of the water touches the stick (1). Measure the height from that water surface to the top of the stick (2), and repeat that measurement below the water surface on a vertical line dropped from the top of the stick.
Practice. — Find surface of water when it touches post (at 1). Draw vertical from top of post. Find surface of water beneath top (at 2). Measure distance from top of post to water surface 3-2.
Reflection of inclined planes. — We saw that the reflection of lines which are in Nature level tend to the same V.P. (Fig. 283) as the originals. It is interesting and possibly useful to notice that the reflection of an inclined plane tends to a V.P. of a plane lying in the reverse direction (provided both are at the same angle). Thus the " uphill " V.P. of a gable roof serves for one side of the roof itself and for the reflection — of the other side ; while the " downhill " V.P. acts in the same way (Fig. 289).
The tip of the distant tower is reflected, its body and the hill are not. The reason being that land occupies the surface where the reflection would come.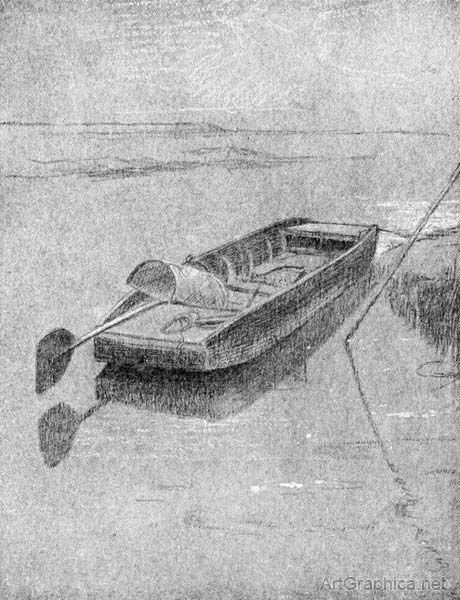
Reflection on a sloping surface. — When a sloping surface such as wet sand gives a reflection the image will not be under the object, as is the case in still water, but it will be inclined to one side (Fig. 295). Its divergence from the vertical position will be slight if the sand is nearly level, and more pronounced on a steeper slope.
One sees that tree and sky might be reflected alternately. His picture therefore would be like Fig. 299, the closeness of the reflection lines in the distance being partly due to their foreshortening. In part also to the fact that the near sides of the distant ripples might catch the reflection of the tree (from the angle they are seen at), instead of reflecting the sky as the near ones would do.
 |
Online Art Books
Perspective for Artists Art Lessons Free Art Books Art Shop Art Links  
 |
